This is a preliminary experiment in putting my lectures up on the Web. For the more visual lecturing I do, i.e. the more stats/research oriented, I tend to create a series of overheads and a handout using Microsoft Powerpoint. Unfortunately it appears to be rather difficult to get good quality conversion of that format to HTML. You can get the text across via RTF and the Microsoft Internet Assistant for Word for Windows 6.0 but graphics can only be saved a slide at a time (and the whole slide, including headings) to .WMF format and then converted to .GIF using (in my case, HiJaak Pro). The results are awful.

However, here for those who may want to amuse themselves, or perhaps even teach themselves some statistics. Is the material from the two lectures I give on the biennial Guildford revision course for psychiatrists about to sit their Part II M.R.C.Psych. exams. I'd be amused to receive feedback to: me [if your HTML browser doesn't support "mailto:" then use a mail package and send to: C.Evans@sghms.ac.uk]

I'll work on Microsoft and the HiJaak people to see if I can improve on the quality of the graphics and will be looking into the feasibility of putting things up using the Adobe Acrobat .PDF format instead of HTML in the near future.

Epidemiology, stats. & research methods for the M.R.C.Psych.

Relationship between sample & population

samp.gif

Sadly this file has converted very badly to GIF format. It shows the relationships between observations (single woman on left!), samples (gaggle in middle) made up of observations and, at least in theory, drawn at random from population (e.g. British adults!)

Sample parameters and population parameters

Sampling and confidence intervals

N.B. difference between C.I. and variance or s.d.:

(that the s.d. is a description of scatter of observations in the sample, whereas the C.I. is an estimate of the location of a parameter in the population from which the sample was taken) 

n=100    mean = 15.5    s.d. = 5.1    95%CI = 14.5 to 16.5
n=1000   mean = 15.5    s.d. = 5.1    95%CI = 15.2 to 15.8
n=10000  mean = 15.5    s.d. = 5.1    95%CI = 15.4 to 15.6

Confidence intervals continued

95% C.I. for sample rate of .1

      n      95% C.I.
     10    .0025 to .45
     20    .012  to .32
     40    .028  to .24
     50    .033  to .22
     70    .041  to .20
    100    .049  to .18
    200    .062  to .15
    500    .075  to .13
  1,000    .082  to .12
  5,000    .092  to .11
 10,000    .094  to .11
100,000    .098  to .102

95% C.I. for sample rate of .1

samp1.gif

This should show the last set of figures as a plot. The axes have been completely lost in translation but I hope it still gives a flavour of the narrowing of the 95% confidence interval as the sample size increases (from Left to Right).

95% C.I. for a mean - simulation of a classical psychopharmacology study ("experiment")

expt.gif

This converted even less satisfactorily than the last two graphics. This shows how the pool of depressed subjects are split into two samples (by randomisation), their depression scores are noted, then, double-blind, one group get active compound and the other placebo for a suitable period after which their depression scores are again noted. The dependent variable to be analysed will be the difference between the two scores so a negative will indicate success: a reduction in depression.

Simulation of a two group comparison study

n = 10

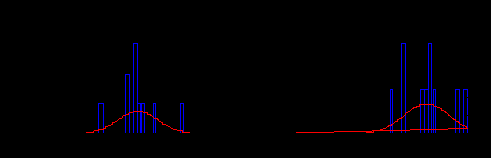
n10.gif

This has converted so badly it seems scarcely worth the candle. It is supposed to show two samples each of n=10 one with a group of drops representing the active compound, the other the placebo where the samples were made on the assumptions shown in the definition above. This particular run of the simulation gives rise to the 95% confidence intervals below.

30 simulations
n = 10

n10c.gif

This shows a the confidence intervals for a number of runs of the simulation.

n = 100

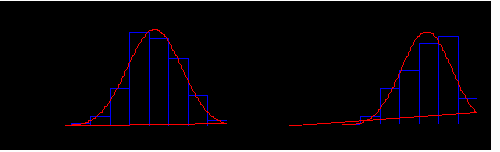
n100.gif

Another terrible conversion. It shows the two samples now with n=100 but still with the same population model. This run of the simulation gives rise to the 95% confidence intervals below.

30 simulations
n = 100

n100ci.gif

Confidence intervals and their assumptions

Confidence intervals are calculated on a model of the study with assumptions

Erotomania & the erotic, delusional transference

Inferential statistics "hypothesis testing", "tests"

Assumptions underpinnning inferential statistics

Test the probability of getting results as interesting as you did given:

If this is less than a certain level (chosen in advance) ...
... the result is declared "significant"

... i.e. the probability of deciding that an effect is "significant" given that the null hypothesis were true for the population

The meaning of "significant" or "p < .05"

The probability of a result as marked as this was lower than 1 in 20 if the null hypothesis (and other assumptions) were true

Null hypotheses

So what's an "alternative hypothesis"?

Alternative hypotheses, type II error rates and statistical power

Given a small study and/or a weak "true" population effect the type II error rate is often very high (.9 for many published "NS" results)

Statistical power

Statistical power is the probability

Statistical power is:

As statistical power has generally been neglected, confidence intervals are replacing p values as they show how large an effect you could be missing

Confidence intervals and "significance" testing

Historically two very different approaches to the problem and there was much acrimonious argument between protagonists of the two approaches

Research frames likely in the exam

A linked set of questions

"How many psychiatric registrars are depressed?"

Quality of measurement - 1 scaling

(N.B. Binary measurements are not easy to classify)

Quality of measurement - 2

Qualities of a binary measure of caseness

qualities that are independent of prevalence

more clinically useful qualities that are dependent on prevalence

indications of lack of contamination

The four screening numbers: a,b,c,d

"True" status Score on test
-ve +ve total
non-case a b a+b
case c d c+d
total a+c b+d a+b+c+d = n 

          a = true negatives               b = false positives
          c = false negatives              d = true positives
sensitivity = d/(c+d)            specificity = a/(a+b)
        PPV = d/(b+d)                    NPV = a/(a+c)




PPV = "Positive predictive value", probability a positive test result will be a case
NPV = "Negative predictive value", probability a negative test result will be a non-case

Reliability

Evidence that the measure is not contaminated by random variation

Validity

The "multiple tests" issue

Distributional assumptions

For M.R.C.Psych. purposes there are two different classes of statistical test

Parametric vs. non-parametric

Matching "tests" to problems

Matching "tests" to problems (contd.)

between non-Gaussian variables - Spearman or Kendall correlation coefficients (latter better if many ties which is often the case on short ordinal ratings)

"Robustness" of statistical tests

parametric tests are often robust (i.e. continue to give about the right type I and II error rates) for distributions that are only roughly Gaussian

Multivariate statistics

The one fairly unproblematical one is internal reliability (coefficient alpha): the proportion of common variance in a set of items