Confidence interval around Spearman correlation coefficient

CECPfuns package Correlation Confidence intervals Non-parametric statistics Rank methods

Explores four methods of estimating a CI around an observed Spearman correlation.

Chris Evans https://www.psyctc.org/R_blog/ (PSYCTC.org)https://www.psyctc.org/psyctc/
2023-11-27

Shiny app

There is now a shiny app using this function here.

This post

Until last week (November 2023!) if I wanted a confidence interval (CI) for a Spearman correlation given the n that created it I used an analytic, parametric method which is actually for the Pearson correlation and I think I was not alone in doing that. However, I have just discovered that there are better approaches and that work on them goes back to the mid 20th Century. Ooops.

They are all approximations that drew on parametric models and if you have raw data, you are far better off using a bootstrap method to get your CI. However, if you are looking at a Spearman correlation in the literature and only have that and the n then you can get a CI but you seem to have a choice of four ways of doing this.

So here are the 95% CIs for observed correlations of zero, .5 and .8 for n from 8 to 100.

Show code 
tibble(n = list(8:100), rs = list(.8, .5, 0)) %>%
  unnest_longer(rs) %>%
  unnest_longer(n) %>%
  rowwise() %>%
  mutate(CIGBW = list(getCISpearman(rs, n, Gaussian = TRUE, FHP = FALSE)),
         CItBW = list(getCISpearman(rs, n, Gaussian = FALSE, FHP = FALSE)),
         CIGFieller = list(getCISpearman(rs, n, Gaussian = TRUE, FHP = TRUE)),
         CItFieller = list(getCISpearman(rs, n, Gaussian = FALSE, FHP = TRUE))) %>%
  ungroup() %>%
  unnest_longer(col = starts_with("CI"), simplify = FALSE) %>%
  rename(limit = CIGBW_id) %>%
  select(-ends_with("_id")) %>%
  select(n, rs, limit, everything()) -> tibCLs

# tibCLs %>%
#   mutate(diffGauss = CIGBW - CIGFieller,
#          sqDiffGauss = diffGauss^2,
#          difft = CItBW - CItFieller,
#          sqDifft = difft^2) %>%
#   summarise(across(diffGauss : sqDifft, mean))

tibCLs %>%
  pivot_longer(cols = starts_with("CI")) %>%
  rename(method = name) %>%
  mutate(Method = case_when(
    method == "CIGBW" ~ "B&W, Gaussian",
    method == "CItBW" ~ "B&W, t dist.",
    method == "CIGFieller" ~ "FH&P, Gaussian",
    method == "CItFieller" ~ "FH&P, t dist."),
    approx = if_else(str_detect(Method, fixed("B&W")), "B&W", "FH&P"),
    distribn = if_else(str_detect(Method, fixed("Gaussian")), "Gaussian", "t dist.")) -> tibCLsLong

ggplot(data = tibCLsLong,
       aes(x = n, y = value, colour = method, shape = method))  +
  facet_grid(rows = vars(rs)) +
  geom_point(size = .4) +
  geom_hline(aes(yintercept = rs)) +
  ylim(c(-1, 1))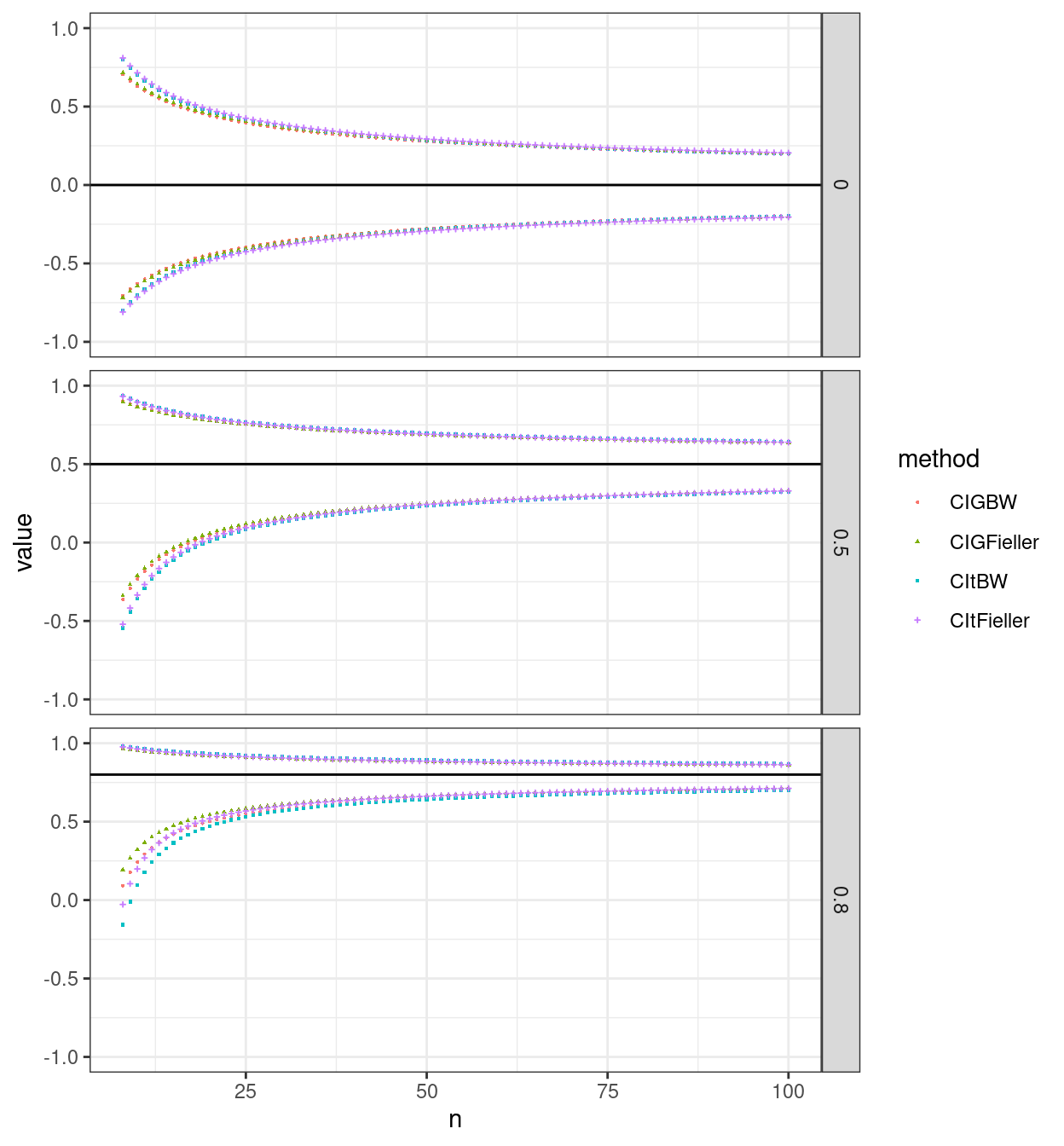

That illustrates several things:

So here is the same plot but just for n from 8 to 15.

Show code 
tibCLsLong %>%
  filter(n <= 15) -> tmpTib

ggplot(data = tmpTib,
       aes(x = n, y = value, colour = method, shape = method))  +
  facet_grid(rows = vars(rs)) +
  geom_point(size = .4) +
  geom_hline(aes(yintercept = rs)) +
  ylim(c(-.85, 1))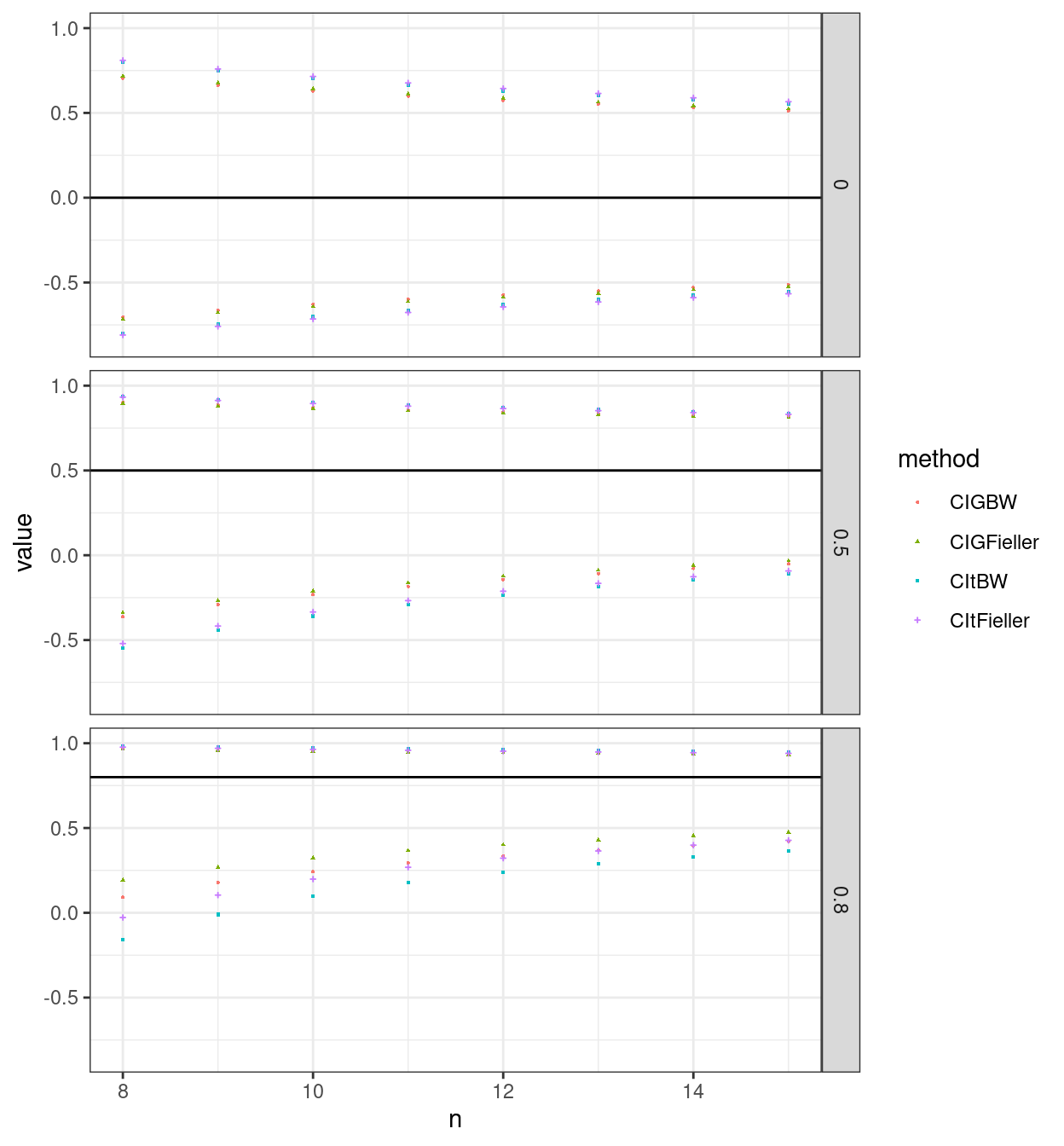

The four methods involve two different changes: the approximation to the standard error of the correlation and whether to look that up against the Gaussian distribution or against the t distribution with df = n - 2. The next two plots facet the issues in the two possible different orders.

This first plot pulls the issue of looking up against the Gaussian or t distributions to the columns in the facetted plot allowing a clearer comparison of the two approximations to the SE of the correlation.

Show code 
ggplot(data = tibCLsLong,
       aes(x = n, y = value, colour = approx))  +
  facet_grid(rows = vars(rs),
             cols = vars(distribn)) +
  geom_point(size = .4) +
  geom_hline(aes(yintercept = rs)) +
  ylim(c(-1, 1))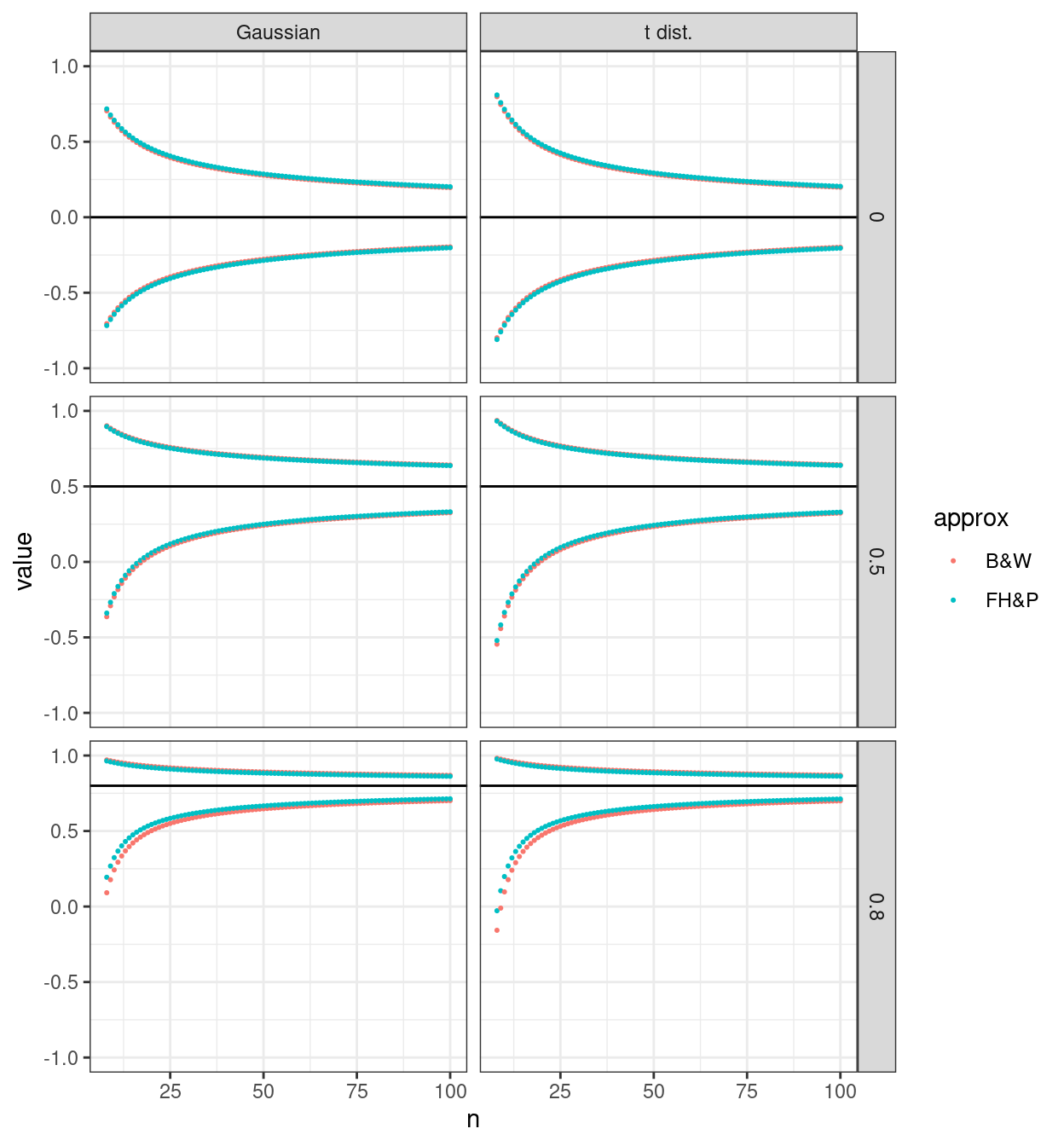

That seems to show fairly clearly that for the zero correlation case the B&W, i.e. the Bonett & White (2000) approximation gives slightly tighter CIs than the FH&P, i.e. the Fieller, Hartley & Pearson (1957) one but that the approximations have the reverse relationship with CI widths for the non-zero correlations.

This next plot makes it easy to look at how the choice of lookup, against the Gaussian or the t distributions affects the CIs.

Show code 
ggplot(data = tibCLsLong,
       aes(x = n, y = value, colour = distribn))  +
  facet_grid(rows = vars(rs),
             cols = vars(approx)) +
  geom_point(size = .4) +
  geom_hline(aes(yintercept = rs)) +
  ylim(c(-1, 1))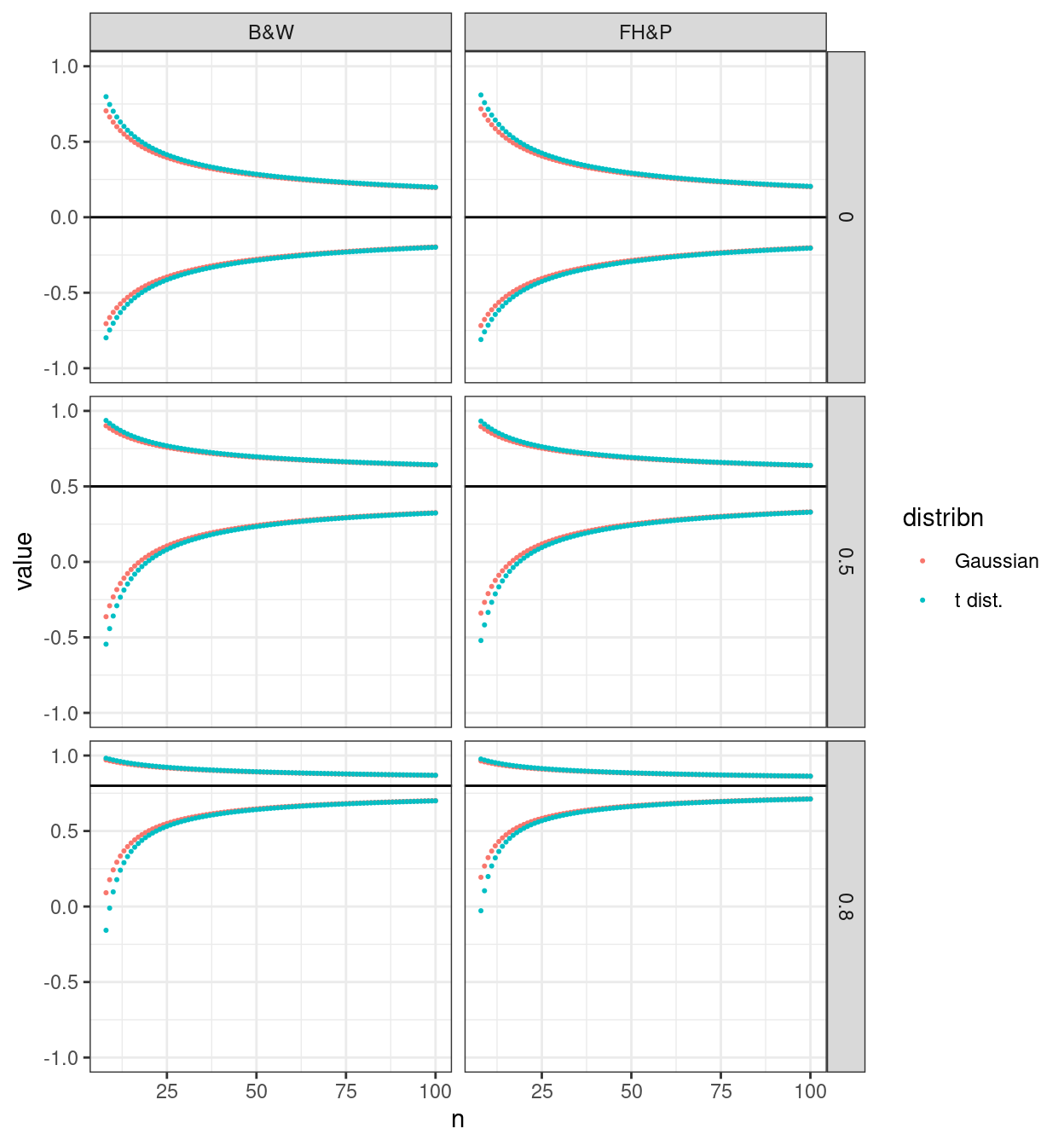

So the Gaussian method gives tighter CIs. However, simulation work I think suggests that these are slightly too tight and that the t distribution method gives coverage closer to 95% in simulations.

Summary

Geeky stuff

This compares the ordering of the CLs from the four methods. It’s pretty geeky as realistically the differences don’t matter for typical therapy/MH work but I have kept this because it interests me and I like the use of order() in the code, but this is angels on the head of a pin stuff!

Show code 
tibCLs %>% 
  filter(limit == "LCL") %>%
  filter(n <= 10) %>%
  rowwise() %>%
  arrange(rs, n, limit) %>%
  mutate(rs = sprintf("%3.1f", rs)) %>%
  select(rs, n, limit, CItFieller, CItBW, CIGFieller, CIGBW) %>%
  as_grouped_data(groups = "rs") %>%
  flextable() %>%
  colformat_double(digits = 4)

rs

n

limit

CItFieller

CItBW

CIGFieller

CIGBW

0.0

8

LCL

-0.8099

-0.7984

-0.7175

-0.7047

9

LCL

-0.7590

-0.7467

-0.6771

-0.6641

10

LCL

-0.7150

-0.7022

-0.6427

-0.6296

0.5

8

LCL

-0.5207

-0.5451

-0.3391

-0.3630

9

LCL

-0.4174

-0.4419

-0.2678

-0.2907

10

LCL

-0.3346

-0.3585

-0.2102

-0.2321

0.8

8

LCL

-0.0280

-0.1573

0.1937

0.0913

9

LCL

0.1043

-0.0105

0.2681

0.1774

10

LCL

0.1986

0.0969

0.3238

0.2426

That shows that the ordering of the lower CLs is not consistent across observed correlations even for that limited range of n. Here’s the same for the UCL.

Show code 
tibCLs %>% 
  filter(limit == "UCL") %>%
  filter(n <= 10) %>%
  rowwise() %>%
  arrange(rs, n, limit) %>%
  mutate(rs = sprintf("%3.1f", rs)) %>%
  select(rs, n, limit, CItFieller, CItBW, CIGFieller, CIGBW) %>%
  as_grouped_data(groups = "rs") %>%
  flextable() %>%
  colformat_double(digits = 4)

rs

n

limit

CItFieller

CItBW

CIGFieller

CIGBW

0.0

8

UCL

0.8099

0.7984

0.7175

0.7047

9

UCL

0.7590

0.7467

0.6771

0.6641

10

UCL

0.7150

0.7022

0.6427

0.6296

0.5

8

UCL

0.9323

0.9366

0.8960

0.9013

9

UCL

0.9127

0.9175

0.8794

0.8849

10

UCL

0.8950

0.9003

0.8648

0.8705

0.8

8

UCL

0.9769

0.9822

0.9641

0.9708

9

UCL

0.9700

0.9761

0.9581

0.9653

10

UCL

0.9637

0.9705

0.9528

0.9603

Just to confirm that I turned those limits into rank order across the four methods as shown here for the LCLs and n from 8 to 15.

Show code 
tibCLsLong %>%
  filter(limit == "LCL") %>%
  filter(n < 16) %>%
  group_by(rs, n) %>%
  mutate(order = order(value)) %>%
  ungroup() %>%
  select(-c(value, Method, approx, distribn)) %>%
  # mutate(rowN = row_number()) %>%
  pivot_wider(names_from = "method", values_from = "order") %>%
  mutate(rs = sprintf("%3.1f", rs)) %>%
  as_grouped_data(groups = "rs") %>%
  flextable()

rs

n

limit

CIGBW

CItBW

CIGFieller

CItFieller

0.8

8

LCL

2

4

1

3

9

LCL

2

4

1

3

10

LCL

2

4

1

3

11

LCL

2

4

1

3

12

LCL

2

4

1

3

13

LCL

2

4

1

3

14

LCL

2

1

4

3

15

LCL

2

1

4

3

0.5

8

LCL

2

4

1

3

9

LCL

2

4

1

3

10

LCL

2

4

1

3

11

LCL

2

4

1

3

12

LCL

2

4

1

3

13

LCL

2

4

1

3

14

LCL

2

4

1

3

15

LCL

2

4

1

3

0.0

8

LCL

4

2

3

1

9

LCL

4

2

3

1

10

LCL

4

2

3

1

11

LCL

4

2

3

1

12

LCL

4

2

3

1

13

LCL

4

2

3

1

14

LCL

4

2

3

1

15

LCL

4

2

3

1

Some of the differences in the LCL values that led to those orderings may have been tiny but it’s clear that the methods aren’t consistently ordering the LCLs within a given observed correlation nor are the orders the same for the different observed correlations.

Acknowledgements

Thanks to all those authors.

Reuse

Text and figures are licensed under Creative Commons Attribution CC BY-SA 4.0. The figures that have been reused from other sources don't fall under this license and can be recognized by a note in their caption: "Figure from ...".

Citation

For attribution, please cite this work as

Evans (2023, Nov. 27). Chris (Evans) R SAFAQ: Confidence interval around Spearman correlation coefficient. Retrieved from https://www.psyctc.org/R_blog/posts/2023-11-27-cispearman/

BibTeX citation

@misc{evans2023confidence,
  author = {Evans, Chris},
  title = {Chris (Evans) R SAFAQ: Confidence interval around Spearman correlation coefficient},
  url = {https://www.psyctc.org/R_blog/posts/2023-11-27-cispearman/},
  year = {2023}
}