At times in the past I have found the idea of “odds” and odds ratios (the better term of the two) a bit anxiety provoking but writing this has helped and I hope it helps others. These are just another way of expressing probabilities or rates. The key thing about them is that the arithmetic of handling them is much easier than that to handle probabilities. That can seem counterintuitive but it’s true and gamblers know it and use it.
Details #
If the probability of something, or the rate of something happening is p then the odds ratio of it is \(\frac{p}{1-p}\). So if the rate of early termination of therapies in a service is 10% the odds for early termination are \(\frac{.1}{.9} \cong .11\). (That symbol \(\cong\) means “approximately equal to”.)
This means that if the rate or probability of something is exactly 50:50, i.e. 50%, i.e. .5 then the odds ratio is \(\frac{.5}{1-.5} = \frac{.5}{.5} = 1\). This means that something that has a rate of over .5 has an odds ratio above 1 and something that has a rate of under .5 has an odds that is under 1, i.e. is a fraction.
At least in gambling on horse racing this is expressed a bit confusingly but uses the same idea. If a horse is said to have “odds of 200” this actually means that our odds ratio is 1/200 and the probability of the horse winning the race is
$$\frac{\frac{1}{200}}{1 + \frac{1}{200}}=\text{0.00497514}$$
(Because
$$\text{probability} = \frac{OR}{1 + OR}$$
That value of 0.00497514 is very close to .005, to 1/200 which illustrates that as odds ratios get smaller, i.e. down to 1/200 and beyond, the differences between an OR and the corresponding probability get very small.
So how does the relationship between odds ratios and probabilities look? #
Like this:
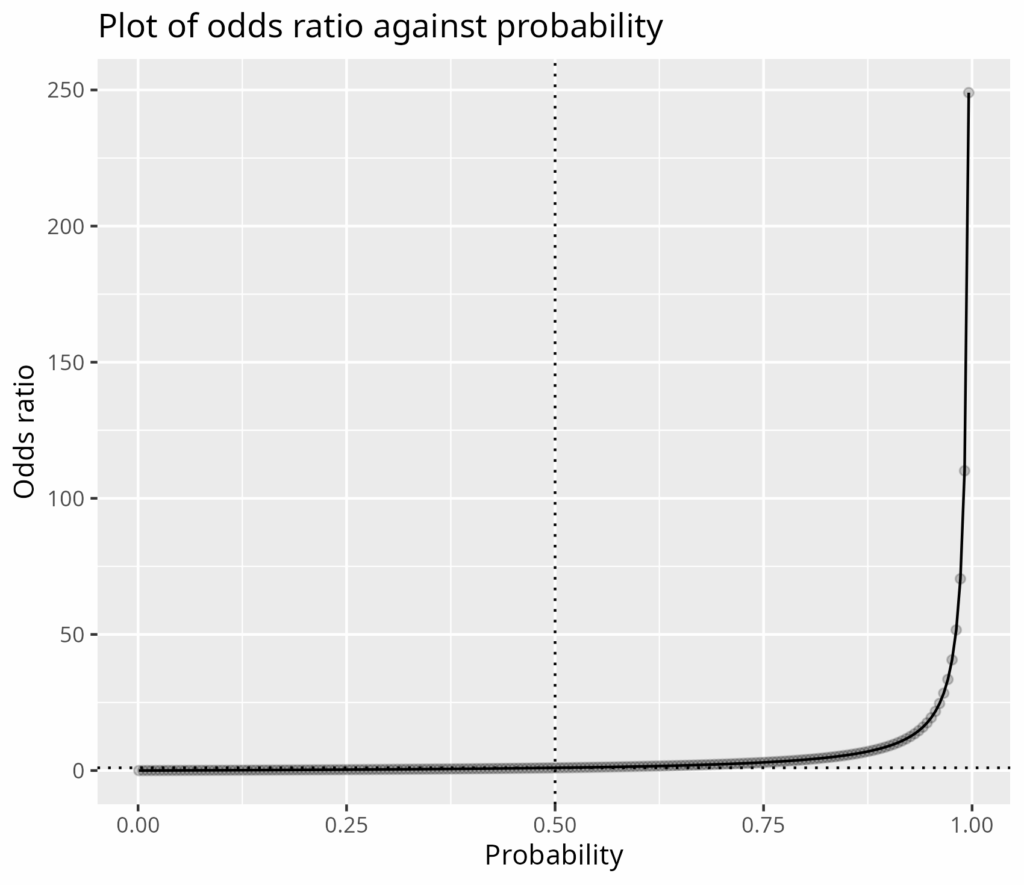
You can see that the odds ratio is not dissimilar to the probably for low probabilities increasingly only slowly through that point (marked by the dotted lines) where the probability reaches .5 and the odds ratio is 1.0. However, you can see that the odds ratio starts to rocket higher as the probability gets higher.
Here’s the other way around: probabilities plotted against odds ratios.
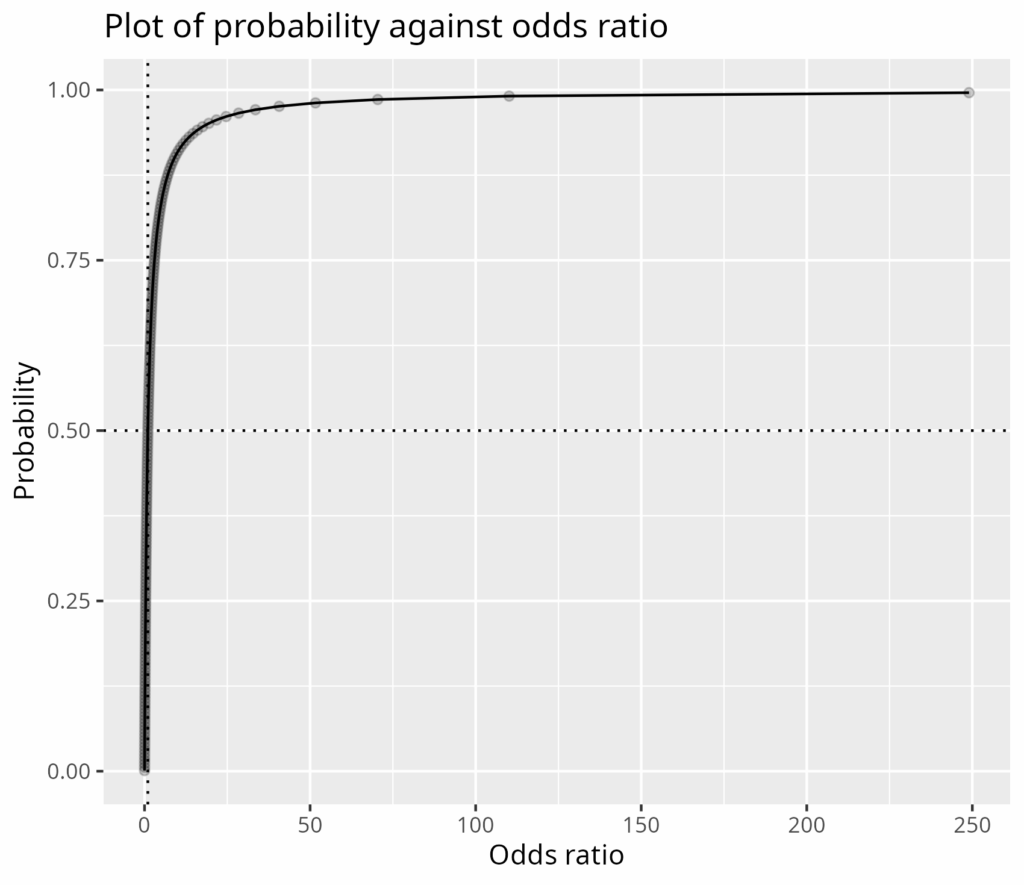
That’s the same relationship but mirrored around the leading diagonal (i.e. mirrored around a line from the botton left of the plot to the top right.
Why is this useful? #
Because if we have some predictor that changes the rate or probability of something happening and we know its likelihood ratio (LR) the odds of the thing happening given the presence of the predictor are simply the odds when we didn’t know about the predictor multiplied by the predictor’s LR:
$$\text{odds}_{\text{not knowing predictor}}*\text{LR}$$
or more generically:
$$\text{odds}_{post} =\text{odds}_{prior}*\text{LR}$$
i.e. the odds of something once we know the presence of a predictor are the odds before, when we didn’t know about the predictor multiplied by the LR, the likelihood ratio, of that predictor.
That’s much easier to handle than the rather convoluted arithmetic you would have to work that out using probabilities and once we have new odds, we now know that we can get to the probability using that simple equation:
$$\text{probability} = \frac{OR}{1 + OR}$$
Incidentally, in horse race gambling (and in all gambling I think) if a horse is thought to be more likely than 50:50 to win the odds are expressed as “odds on” so if the favourite is said to be a “4 to 1 odds on favourite” it means that the odds of the horse winning are thought to be 4.0 and so the probability of it winning is thought to be 4/5 = .8 = 80%.
Log odds #
You will quite often see odds discussed in terms of “log odds” and “logits”. These are the logarithm (q.v.) of the odds. This shows log odds, and the odds plotted against probabilities. This is also known as “logit scaling”.
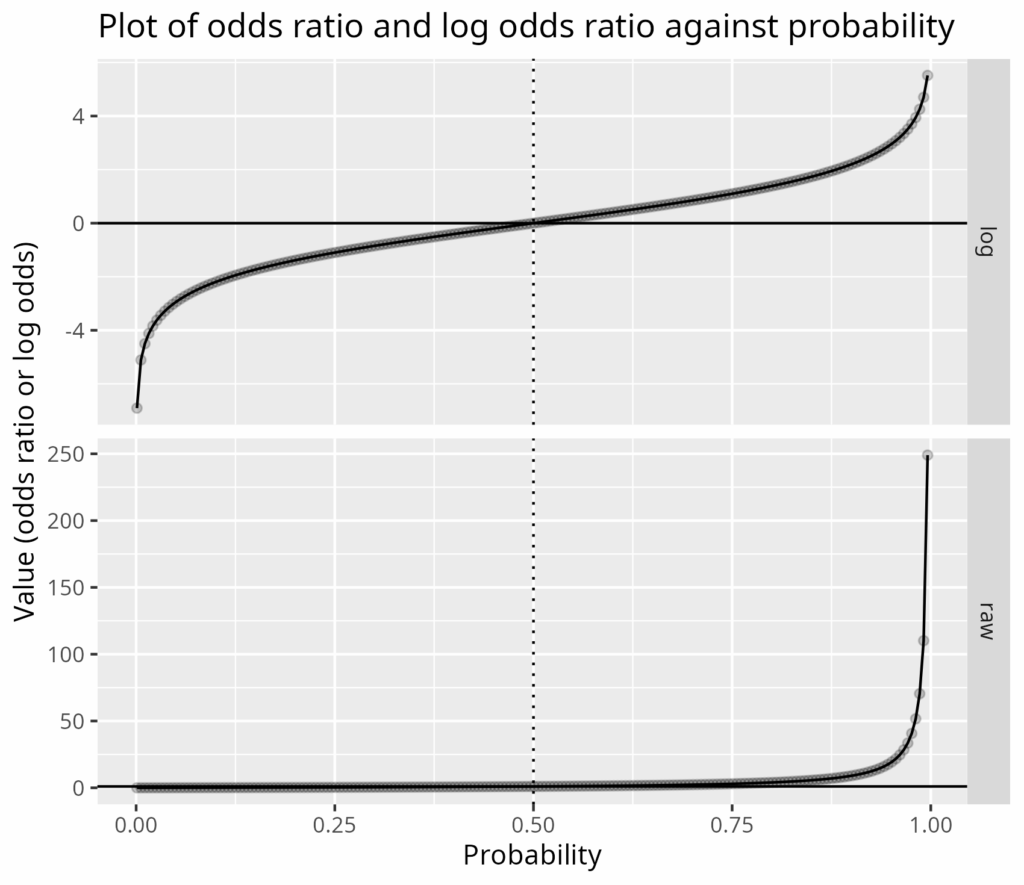
That shows how taking logarithms of odds gives a very different plot and one that is symmetrical around the probability of .5. For statisticians and programmers working with log odds is much easier than working with raw odds though it’s easy to get actual odds from the log odds.
Try also #
- Likelihood ratio
- Logarithms
- Probability
Chapters #
Not covered in the OMbook.
Online resources #
None currently.
Dates #
First created 24.vii.25, updated 27.vii.25 to add log odds and link to entry about logarithms.

