This has been a very influential model for the analysis of responses to multi-item. It has many overlaps with the one-parameter IRT (Item Response Theory, IRT, q.v.) model. A crucial and in some ways contentious difference is that the Rasch model is really a prescription for how a measure should behave and a way of testing its fit to that model whereas IRT models are essentially ways of inferring (rather similar) properties to a measure from a dataset. To some extent this distinction reduces to the idea that Rasch models and exploration of the fit of data to the Rasch model is, in theory, mainly a way of improving questionnaires (and performance tasks) until the responses they get in datasets appear to conform to the model whereas IRT (and all of CCT (Classical Test Theory, q.v.) are statistical ways of looking the fit of the data from responses to models without seeing the models as crucial to claim quality measurement.
Details #
Rasch’s argument was that measurement in the human sciences field should fit that in the physical sciences and fundamentally that responses of different people to items should be solely a function of each person’s location on the scale to be measured. This property is true, or closely approximated to by the measures used in the physical sciences: the measure is independent of the thing measured. (That gets a bit more complex at subatomic, quantum levels and as you move up into relativity but Rasch was not affected that I can see by that issue and, to be fair, it’s a very particular set of issues that, however vital to any fit between theory and observations at subatomic or cosmological scales, isn’t terribly important to everday physical science and its applications.)
The Rasch model assumes that a simple logistic curve relates the probability of answering positively to an item to the difference between the person’s location on the underlying scale to be measured from the location on that same scale of each particular item. This makes the perfect response curves look like this.
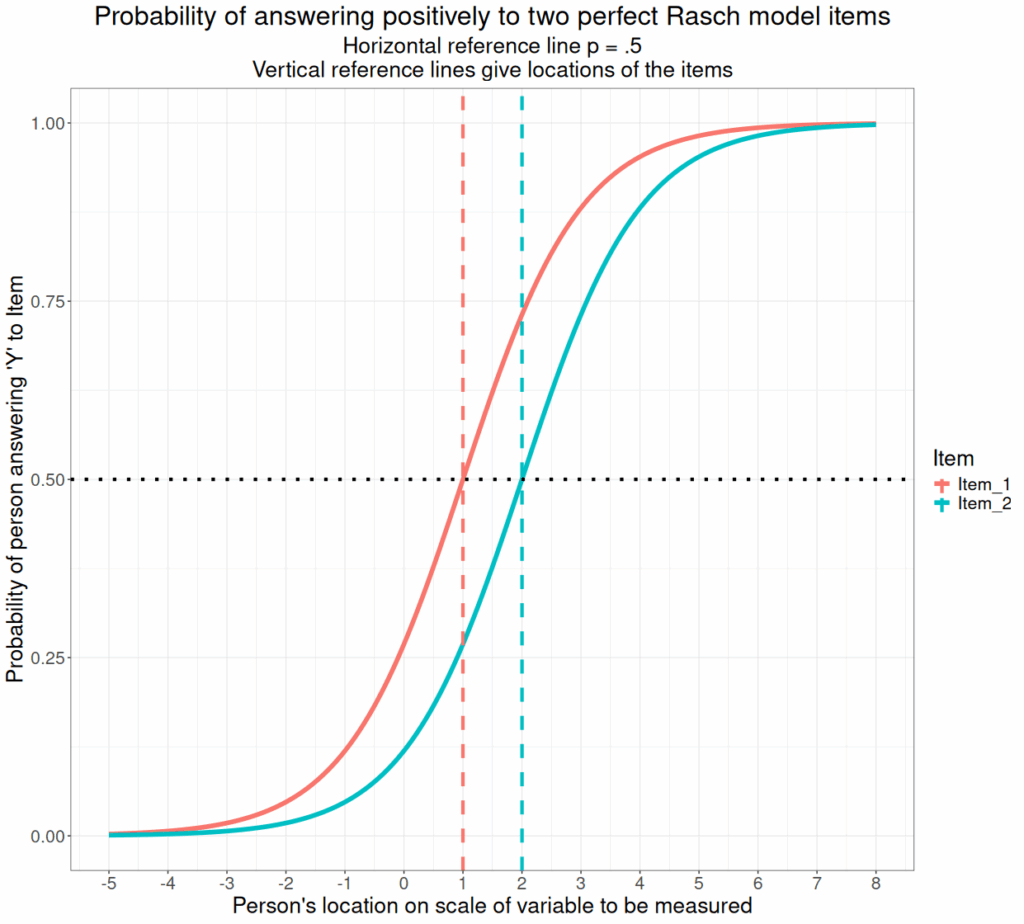
That’s pretty much the same as a typical one parameter IRT model. By making the relationship a function of that difference in location of the person and the item the model emulates the measurement of the physical sciences: the thing measured and the thing measuring are independent of one another.
That may seem counterintuitive when I’m saying that the model uses the difference between the two and that makes no sense in the natural sciences: a weighing scales is not measuring the difference between the weight of the person standing on it and its own weight and we expect all weighing scales, whether very lightweight or heavy to give the same answer. However, it is precisely putting the difference into the equation in the way Rasch did that that says that it is only this difference that matters and that allows you to use the location estimates for the people measured to estimate the locations of the items and vice versa. It is also assuming that this relationship will be the same for all people whenever measured and that nothing else is impinging on the likelihood of any person answering positively other than their location on the scale and the location of the item they are answering.
These are very stringent criteria. It is possible to construct knowledge measures and task performance scales that can fairly close to Rasch measurement qualities but for measures of most mental phenomena this is probably such an unlikely situation that the most zealous Rasch theorists have largely stayed out of our field and the Rasch model only been used rather rarely.
Try also #
- Classical Test Theory (CTT)
- Item Response Theory (IRT)
- Mokken scaling
- Psychometrics
- Reliability
- Unidimensionality
- Validity
Chapters #
Not covered in the OMbook.
Online resources #
None likely.
Dates #
First created 14.v.25.

