The median is the score in a set of scores that divides the distribution in two. So if the scores are 1, 2, 3, 4 and 5 the median is 3 to give a trivial example. Where the distribution of scores is strongly skew (see skew!) the median can be a more useful measure of “central location” than the more commonly used mean (a.k.a. average, or arithmetic mean).
Details #
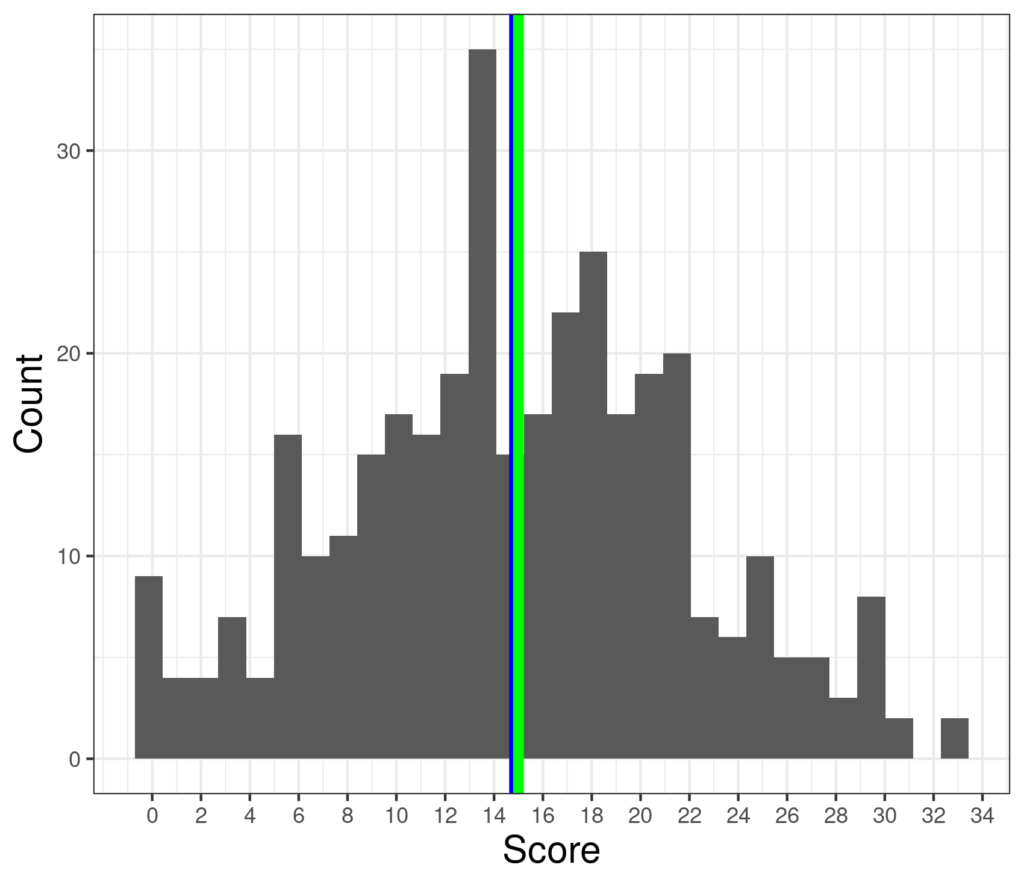
Here is a histogram of fairly symmetrical distribution showing the mean (blue) and median (green) fairly much aligned.
But here is a distribution with a strong positive skew (tail off to the right: to the higher scores) where the median and mean are more separated.
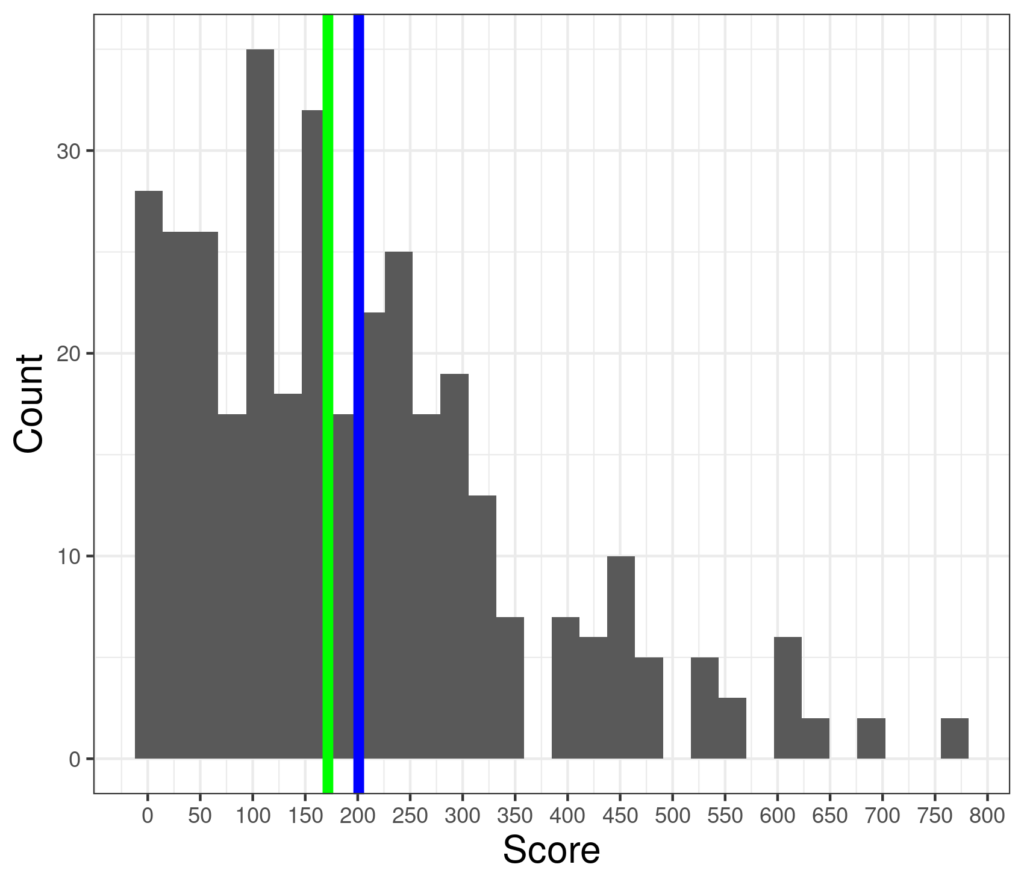
This happens because the rare, but very high scores contribute heavily to the total score and the mean is the total divided by the number of scores. By contrast, the median is always the score (observed or inferred) that separates the distribution into two equal sized halves so is not pulled up by those rare high scores.
Try also #
Mean (average, arithmetic mean)
Skew
Central location
Distribution
Chapters #
Chapter 5
Online applications #
In due course there will be a shiny app to compute the median and other summary statistics for a set of data.
Dates #
Created 1/11/21.

