Reliable change
Reliable change was a concept introduced by the paper: Jacobson, Follette & Revenstorf (1984) “Psychotherapy outcome research: methods for reporting variability and evaluating clinical significance.” Behavior Therapy 15: 336-352 and modified after a crucial correction: Christensen & Mendoza (1986) “A method of assessing change in a single subject: an alteration of the RC index.” Behavior Therapy 17: 305-308.
The best early summary of the method is in Jacobson & Truax (1991) “Clinical significance: a statistical approach to defining meaningful change in psychotherapy research.” Journal of Consulting and Clinical Psychology 59(1): 12-19 hence you sometimes come across this called “Jacobson & Truax RCSC” or “Jacobson & Truax method(s)”. The paper I contributed to this: Evans, Margison & Barkham (1998) The contribution of reliable and clinically significant change methods to evidence-based mental health Evidence Based Mental Health 1:70-72 was one we wrote as we put RCSC fairly centrally in our early thinking about the CORE system. That seems to be regarded as readable introduction to RCSC and I’m happy to send it to anyone who contacts me.
Reliable Change (RC) is about whether people changed sufficiently that the change is unlikely to be due to simple measurement unreliability. You determine who has changed reliably (i.e. more than the unreliability of the measure would suggest might happen for 95% of subjects) by seeing if the difference between the follow-up and initial scores is more than a certain level. That level is a function of the initial standard deviation of the measure and its reliability. If you only have a few observations it will be best to find some typical data reported for the same measure in a service as similar as possible to yours. The reliability parameter to use is up to you. Using Cronbach’s alpha or another parameter of internal consistency is probably the most theoretically consistent approach since the theory behind this is classical reliability theory. By contrast a test-retest reliability measure always includes not only simple unreliability of the measure but also any real changes in whatever is being measured. This means that internal reliability is almost always higher than test-retest and will generally result in more people being seen to have changed reliably.
Thus using a test-retest reliability correlation introduces a sort of historical control, i.e. the number showing reliable change can be compared with 5% that would have been expected to show that much change over the retest interval if there had been no intervention.
I recommend using coefficient alpha determined in your own data but if you can’t get that then I’d use published coefficient alpha values for the measure, preferably from a similar population.
$$SE = SD*\surd(2)*\surd(1-rel)$$
where:
SD1 is the initial standard deviation
rel indicates the reliability
The formula for criterion level, based on change that would happen less than 5% of the time by unreliability of measurement alone, is:
$$RCI = 1.96*SD*\surd(2)*\surd(1-rel)$$
That’s the SE multiplied by 1.96 because 1.96 is the value of Gaussian distribution that includes 95% of its values. Many years ago I wrote a little Perl program to calculate this that would work with cgi-bin form to calculate RCI for you but it was very crude and I have replaced it with a shiny app to do the same. In the unlikely event that anyone wants the old perl code, it’s here.
Clinically significant change
Clinically significant change was introduced in the same 1984 paper by Jacobson, Follette & Revenstorf. This is a complement to reliable change: it’s not about whether the change is greater than might be expected by simple measurement unreliability but solely about the state the person achieves. Clinically significant change is is change that has taken the person from a score typical of a problematic, dysfunctional, patient, client or user group to a score typical of the “normal” population. Jacobson, Follette & Revenstorf (1984) offer three different ways of working this out.
- Their method (A): has the person moved more than 2 SD from the mean for the “problem” group?
$$crit_a = mean(\text{help-seeking-group}) + 2*SD(\text{help-seeking-group})$$
That’s if the measure is a “health” measure i.e. higher scores describe a better state. If its a dysfunction/distress measure where higher scores describe less good states then:
$$crit_a = mean(\text{help-seeking-group}) \;-\; 2*SD(\text{help-seeking-group})$$
- Their method (B): has the person moved to within 2 SD of the mean for the “normal” population? So for a health tuned measure:
$$crit_b = mean(\text{non-help-seeking-group}) + 2*SD(\text{non-help-seeking-group})$$
If the measure is a “dysfunction” or problem measure:
$$crit_b = mean(\text{non-help-seeking-group}) \;-\;2*SD(\text{non-help-seeking-group})$$
Their method (C): has the person moved to the “normal” side of the point that is often referred to as “halfway between the means”. It is halfway between the means only if the standard deviations in each group are the same otherwise it’s:
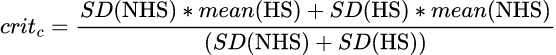
This is the only really defensible method of getting the CSC and it has the nice property that it defines the only cutting point (in the Gaussian model) that makes the misclassification of each group equal, i.e. the rate of non-help-seeking people classified as help-seeking is equal to the rate of help-seeking people classified as non-help-seeking. Again the arithmetic, as you can see, is really trivial but I hate arithmetic so again I wrote a little Perl program to calculate this as an online app. That app is here though I can’t think why anyone would want it! Much more usefully, I have now produced a shiny app that does the same but adds the picture of the cutting points for method c which is here.
Putting them together
When summarising results you are clearly particularly interested in any people who got reliably worse: all good services recognise they don’t always succeed and this is a good criterion on which to select out cases for a some clinical review. Then you are interested in people who got reliably better but not clinically significantly so. This may be because movement into the “normal” range is unrealistic or because your clinic sees people who are not so different from “normal” that that change is easily achieved. Then you are similarly interested in those who got clinically significantly, but not reliably, better. This suggests they were near enough to the boundary between “problem” and “normal” groups to start with that the clinically significant improvement is unreliable (which may mean it likely to relapse). Finally, the people you are interested in most are those who showed both reliable and clinically significant improvement. Those who changed most are clearly the ones you might select for positive clinical case review.
Final caveats
- A worrying number of papers say they are using RCSC but don’t make it clear what method was used for CSC or do say but don’t explain or sometimes even say at all what referential data were used. Similarly, if RC was reported based on the sample data papers rarely say what reliability value was used and why.
- Many papers use RC against some RCI (Reliable Change Index) based on variance and reliability values that didn’t come from the sample. This purports to bring the RC/RCI in line with other referential values: it becomes referential as a value. However, this completely negates the psychometric logic that justifies the calculation of RC in the first place. I don’t like this tendency but confess I’ve done this myself. I think the safe way around this if there is a need for a referential RCI is to report how differently the data look if the RCI based on the sample internal reliability and baseline SD are used to compute it.
- Always remember that measures only measure part of the human condition and don’t always do that well. Such methods should always be used in parallel with other ways of reviewing clinical work.
Page created 4.i.19 pulling together various things from the old psyctc.org site that had first appeared there in and after 1998. Updated for transition from perl to shiny apps 19 to 21.ix.23. All content, text, code and header image (Mont Blanc from Aime2000, French Alps, is by CE and made available under a Creative Commons License. Please feel free to reuse anything here but respect the licence, i.e. give attribution back to here.
