This is a bit geeky but you might come across it in research papers. I confess I love the word but I think we also know it’s the sort of word that people who at least recognise it love to use as it sounds so posh and knowledgeable! Its opposite is homoscedasticity.
Details #
So what does it mean? Just that the variance (q.v.) of a continuous measure in different groups is different. Here’s an example:
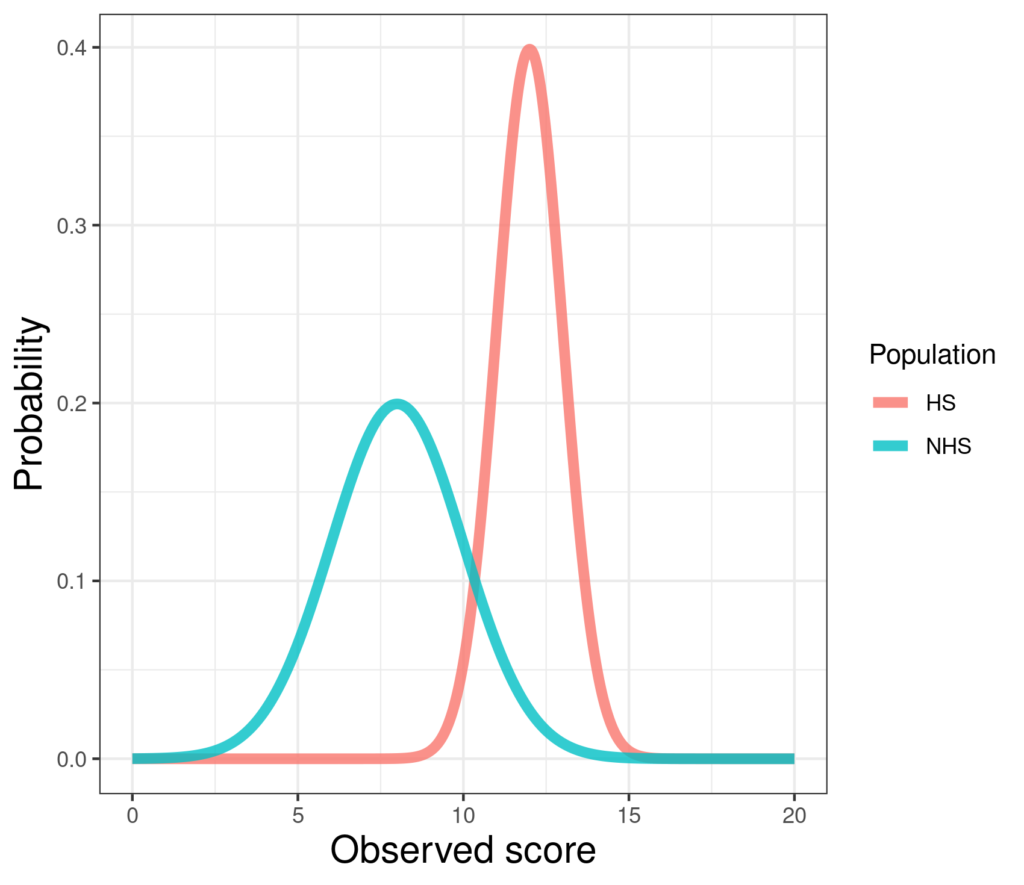
Those are two simulated Gaussian distributions with different means but also different variances. The left hand one, a simulated non-help-seeking population, has mean 8 and standard deviation 2, i.e. variance 4. The right hand one has mean 12 and SD (and variance) 1. (Very simple R code for this here in the Rblog!)
Heteroscedasticity is almost always used in relation to sample data and in relation to testing to see whether the variances in two or more groups of sample data are sufficiently different to suggest that the variances in the populations from which those samples came are also different. So this is NHST (Null Hypothesis Significance Testing) but for variances not means.
Sometimes it is substantively interesting: finding that scores on a measure have a different variance in women than in men (sorry, very binary) may be quite important. Just as important can be finding that the variance of intake scores on a measure have a much higher variance for one service than another should raise some curiosity and further exploration.
Apart from that substantive interest, heteroscedasticity is also important because the NHST for mean group differences like the independent t-test for two groups and the ANOVA (g.v.) for more than two groups have as one of their assumptions that the variances of the groups in the population are the same. When that’s not the case the p values, and hence decisions based on these analyses, can be misleading particularly if group sizes in your data are rather different, say 73 women and 19 men or one service with over 2,000 clients and one with 300. There are tweaks to the tests that can make them more robust to heteroscedasticity but that’s probably getting beyond the remit of the glossary … or perhaps not. I’ll come back to it if people ask! The bootstrap (q.v.) based confidence interval (q.v.) estimation (q.v.!) approach to comparing means across groups is fairly robust to the heteroscedasticity as far as I can see.
Try also #
Bootstrap, bootstrapping
Bootstrap methods
Confidence intervals
Null Hypothesis Significance Testing (NHST)
Inferential testing, ‘tests’
Variance: introduction
Variance: computation and bias
Standard deviation
Robustness & robust tests
Sensitivity analyses
Chapters #
We didn’t put it in the book!
Online resources #
Not yet!
Dates #
First created 21.viii.23, links updated 14.viii.24.
