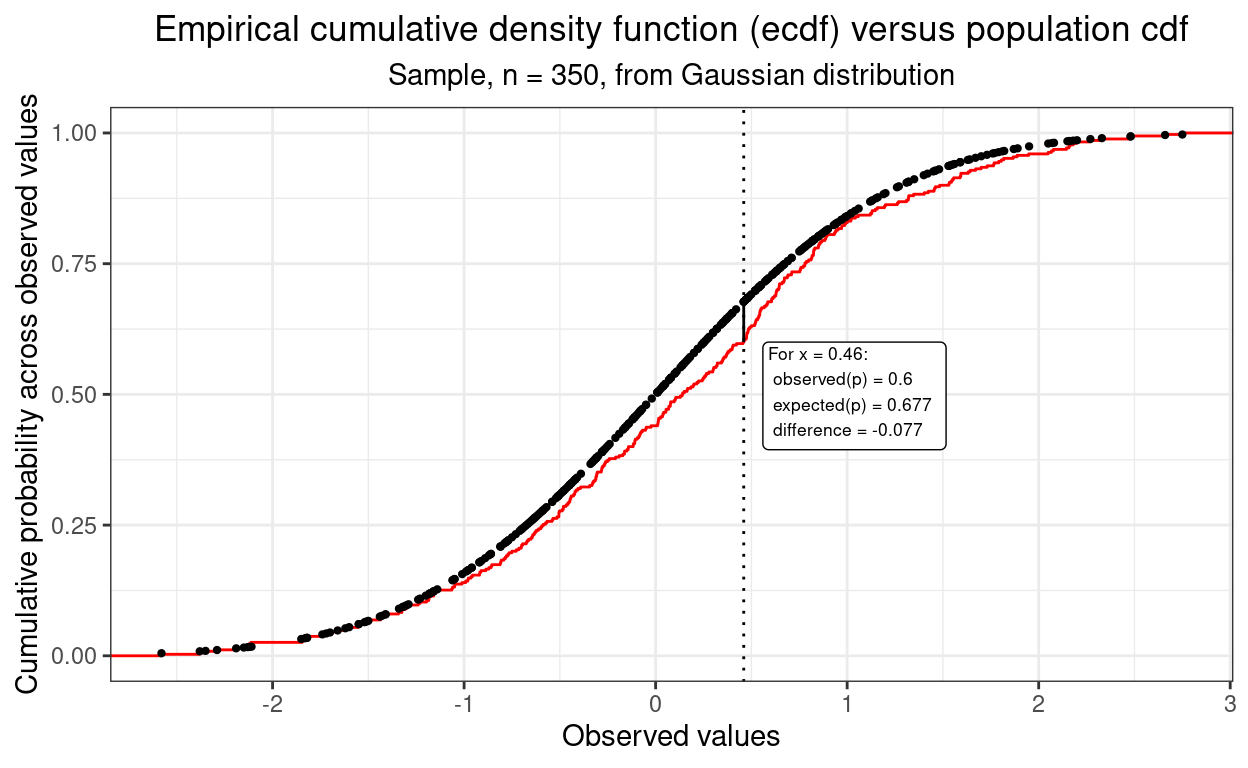
The K-S test is a test of the fit of a univariate (single variable) distribution either against the distribution of another variable (two sample K-S test) or against a theoretically expected distribution (single sample K-S test). It is often used as a test of the fit of the distribution to the famous “bell shaped” Gaussian distribution. (The Gaussian distribution is probably far more often called the “Normal distibution” but I try to avoid that term for the obvious associations and implications that it is normal to find distributions fitting it … which mostly they don’t!)
A test of fit (or misfit) tests whether the shape of the distribution matches the shape of the other distribution, misfit can can take many forms and there are many fit tests of which the K-S test is only one of the earliest and not the best but is easy (ish) to understand.
Details #
Technically the K-S test tests the maximum vertical difference between the cumulative distribution. Go to my Rblog post about it for a pretty full explanation and exploration of it.
Try also #
Distribution shape
Gaussian (“Normal”) distribution
Inferential testing
Null hypothesis testing (NHST)
P value
Parametric tests
Rblog
Statistical assumptions / model
Chapters #
Not specifically mentioned in the OMbook
Online resources #
My Rblog post about the K-S test
Wikpedia page about the K-S test
Dates #
First created 11.xi.23, updated 17.xi.23 adding header graphic and improving cross-referencing.

