This should probably be called “parametric statistics” as it’s not just “tests”, i.e. NHSTs: Null Hypothesis Significance Tests it’s also involved in a lot of confidence interval estimation. The key point is that parametric models were, and sometimes still are, the best way of tackling statistical questions about continuous variable data. The alternative was “non-parametric tests” (logical!) but things are a bit more complicated now with the arrival of bootstrap methods (q.v.).
Details #
The term “parametric” comes from the way that the method turns on being able to summarise the population distribution with just two parameters: the mean and the standard deviation (or the variance which is just the square of the SD). The tests, which include the famous t-test, Analysis of Variance (ANOVA) methods and the Pearson correlation coefficient and most traditional linear and some non-linear regression methods all assume that the data you have is a random sample from infinitely large populations in which the variables have Gaussian (a.k.a. “Normal”) distributions. Like a number of other distributions the Gaussian distribution is defined by just these two parameters. (Other distributions may also be fitted on the basis of just these two parameters and others may need other distributions.)
Here are two large (n = 5,001 in each) simulated samples from Gaussian population distributions.
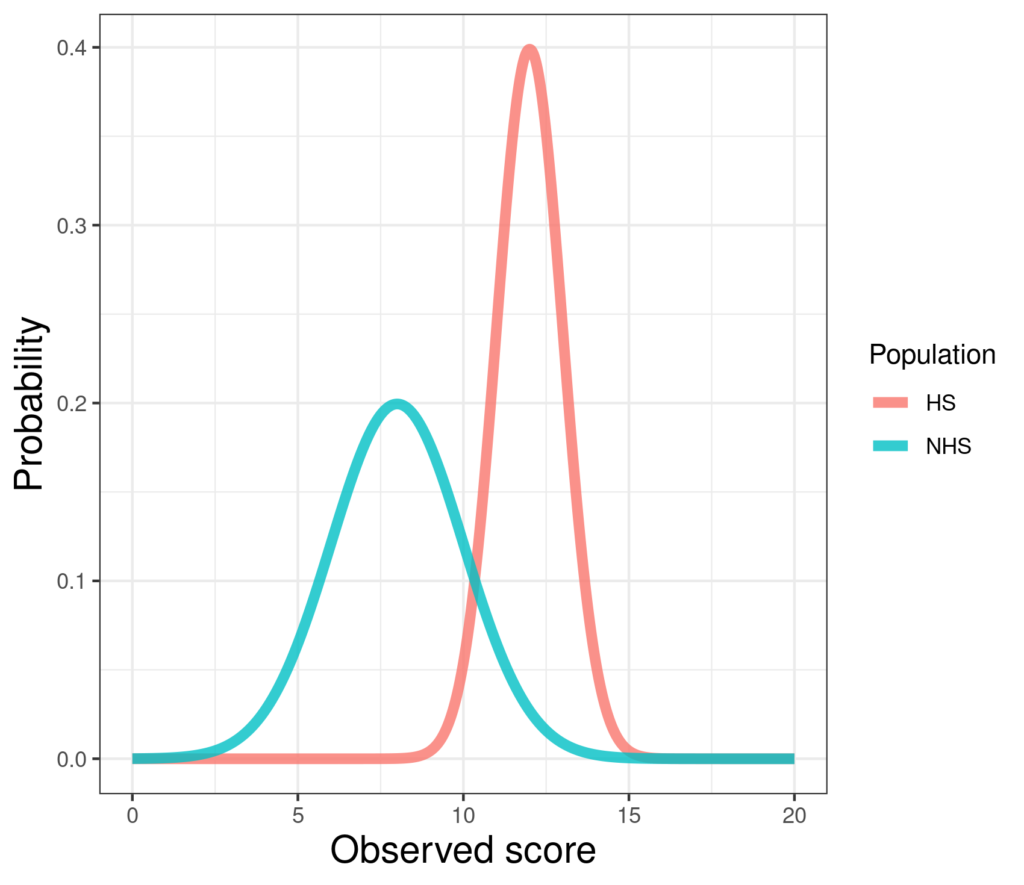
Those look very different but they are entirely defined by their means and SDs. The left hand one, a simulated non-help-seeking population, has mean 8 and standard deviation 2, i.e. variance 4. The right hand one has mean 12 and SD (and variance) 1. (Very simple R code for this here in the Rblog!)
If you make that assumption that the population distributions are Gaussian and that your samples are random sample from those populations (and add some others assumptions) you can use your sample data to estimate how likely it is that you would have seen results as interesting or even more interesting that you did if in the population nothing systematic was happening (the null hypothesis, see that and the NHST entry ). The catch is that if the population distribution is not Gaussian then the conclusions from the analyses can be misleading: parametric tests depend on that assumption and hence the tests are not “robust” to deviations from Gaussian distributions. The challenge is to know how big the deviations from Gaussian have to be before conclusions from the tests can become fundamentally misleading. For some parametric tests, like the t-test, this is relatively simple to explore (but you almost never see comments on that), for others it may be more difficult.
The alternative approach is to use non-parametric tests which make no assumptions about the population distributions. On the face of it this is a no-brainer: if you don’t need to make those, often implausible, assumptions to use non-parametric tests why not just always use them? There are two issues here:
(1) non-parametric tests are never as powerful (see statistical power) as their parametric siblings if the population distributions are Gaussian so you need larger samples to have the same likelihood of detecting a population effect with them than with a parametric test;
(2) more seriously for many of the wide range of parametric tests for all sorts of complex questions about data that are important to us no obvious non-parametric tests exist.
One approach that has been very dominant in psychology and MH has been to look at the distribution of the continuous variable(s) of interest in the sample data and test whether the distributions are significantly different from Gaussian. If not then the argument goes you can go ahead with the parametric test and if they are significantly different from Gaussian you can either see if “transforming” the data can bring them to non-significant deviation from Gaussian and then use the parametric test on the transformed data … or, if there is one, you can use the appropriate non-parametric test.
At first glance that sounds sensible but of course there are catches here:
(1) distributions can deviate from Gaussian in various ways and there are different tests of the sizes of such deviations so this isn’t as simple as it sounds;
(2) probably more fundamentally, if your sample is small the test of fit to Gaussian distribution is weak and will say that the deviations are non-significant even if they are perhaps large enough in the population to really affect the parametric test and, likewise, if the sample is large the tests will show statistically significant deviation from Gaussian (e.g. if there are say only ten possible scores the discontinuous nature of the distribution may show as significant even though the shape of the scores is close to Gaussian and the parametric test in this situation will work fine).
That approach is probably rightly dying out and for many tests/analyses now it is possible to use bootstrap methods to find p values or confidence intervals.
Oh and that brings us to another thing: the focus on the NHST paradigm means that the literature on parametric versus non-parametric methods can read as if the issue only affects NHSTs and not estimation and confidence intervals. That’s simply not true if the CI estimation is parametric e.g. for the traditional way of estimating the CI around an observed mean using the mean, SD and n. However, there’s really no excuse for using parametric methods for that CI and most others now when good statistical software will offer a bootstrap method which is pretty robust to distributions unless they are frankly bizarre.
Try also #
Bootstrapping / bootstrap methods
Confidence intervals
Estimation
Inferential tests
Mean
Non-parametric tests
NHSTs: Null Hypothesis Significance Tests
Paradigms
Chapters #
Touched on in Chapter 5.
Online resources #
Should be building slowly on my shiny server in months to come. Check there as I don’t always have time to add links back to the glossary when I add new apps there.
Dates #
First created 22.viii.23.

