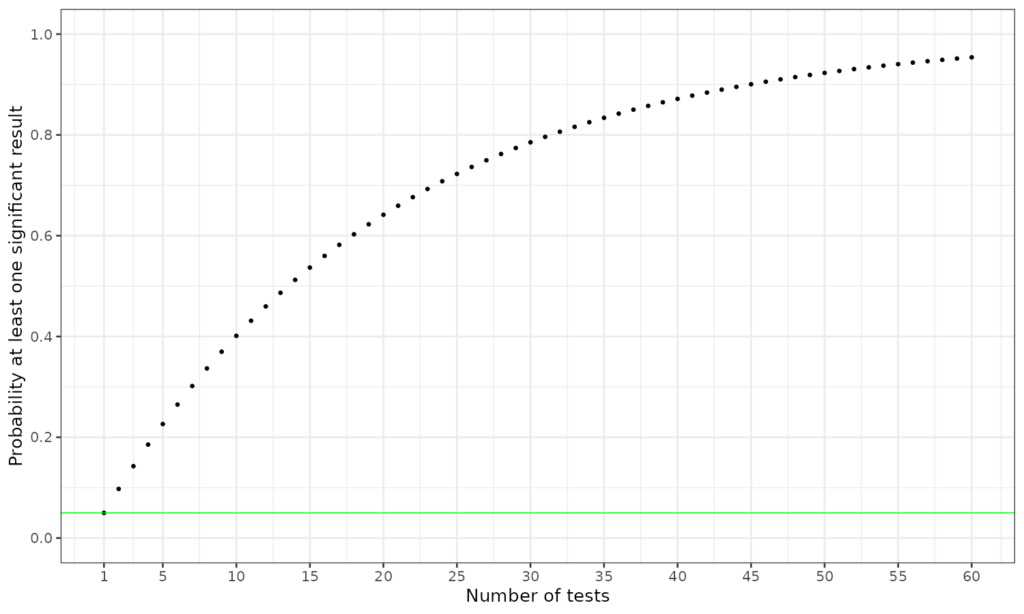
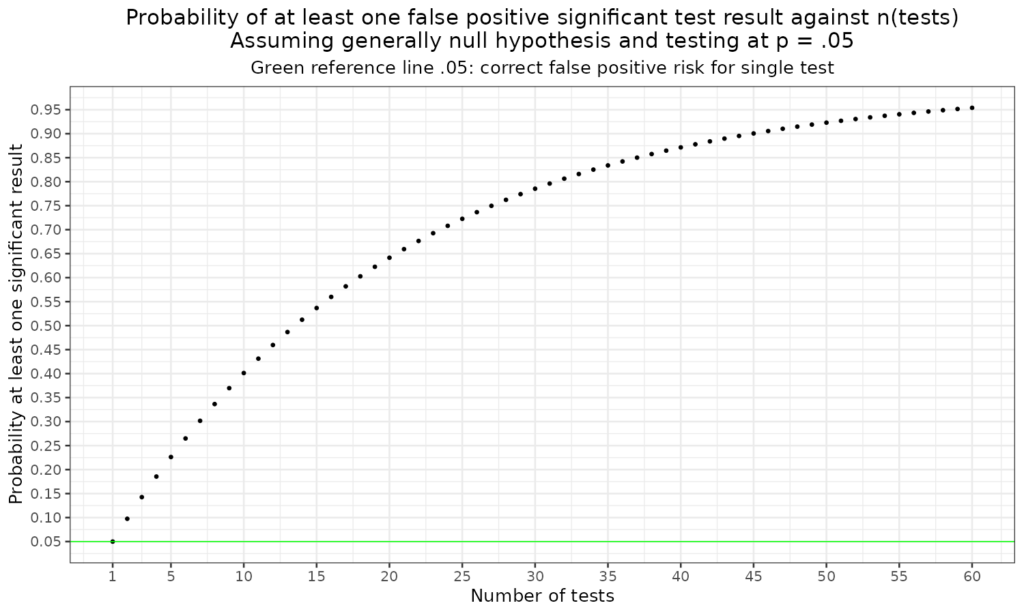
This is an interesting phenomenon. The key idea in statistical “tests” is that before you do a study and plan into it a test of something you set a criterion risk you are willing to run of saying on the basis of your data that something systematic is happening when in fact that is just a “sampling vagary”: your data happened to look interesting in whatever way your test tests, but another sample, another time, wouldn’t. The convention is to set the risk at one in twenty, the famous “p = .05” so you reject the null hypothesis that nothing systematic is happening if you have p < .05 that a result as interesting looking, or more interesting, would have happened by chance sampling from that null hypothesis population in which nothing systematic is happening. This is fine for one test but what happens if you have more than one question of interest. Now you hit the multiple tests problem.
Details #
The problem is that the risk of at least one false positive given that the general null hypothesis is true for the population, i.e. that none of the effects you are testing for is really there, goes up rapidly from .05 for a single test, to .0975 for two tests, .143 for three and so on. The header graphic shows this. This labels and titles it.
Here is the full table of that.
This is actually basic binomial distribution: here are the probabilities of the numbers of falsely significant tests assuming the general null applies and the criterion for significance is p < .05.
The “NA” entries there are the R convention for missing data: “Not Available” and clearly you can’t have three significant tests if you only did two tests! The columns that do have values are showing the probabilities of finding that number of tests significant given the general null model. The probabilities for one or more significant tests, i.e. taking the sum across the those columns give the probabilities of at least one significant test that I showed for up to 60 tests in the earlier table.
Clearly this means that if the literature is full of work where more than one test was reported and all were reported using the p < .05 criterion then there is a worryingly high likelihood, greater than p = .05, perhaps much greater than that, that some of these supposedly significant findings are spurious.
This doesn’t rule out doing multiple tests on data: if you have many questions of interest and have collected a lot of data with the support of the clients who contributed the data then there’s a clear need to do the tests. There are no perfect solutions to this “multiple tests problem” though. Careful workers at least report the risk, more sophisticated options are to apply corrections to remove the problem. The most famous of these is the Bonferroni correction which is a very thorough correction as it really does remove the problem but with the catch that it reduces statistical power dramatically as the number of tests you conduct goes up. There are other corrections that are sometimes robust enough and are less conservative than the Bonferroni correction. This is is a tricky area where ideally you work with an experienced researcher and/or a statistician.
Try also #
Bonferroni correction
Binomial distribution
Null hypothesis testing
Null hypothesis significance testing (NHST) paradigm
Population
Sampling and sample frame
Chapters #
Probably should have been in Chapter 5 … but you can’t have everything in a small book!
Online resources #
Rblog post about the Bonferroni correction
Shiny app to look at costs of the correction in terms of statistical power
Dates #
First created 20.xi.23

