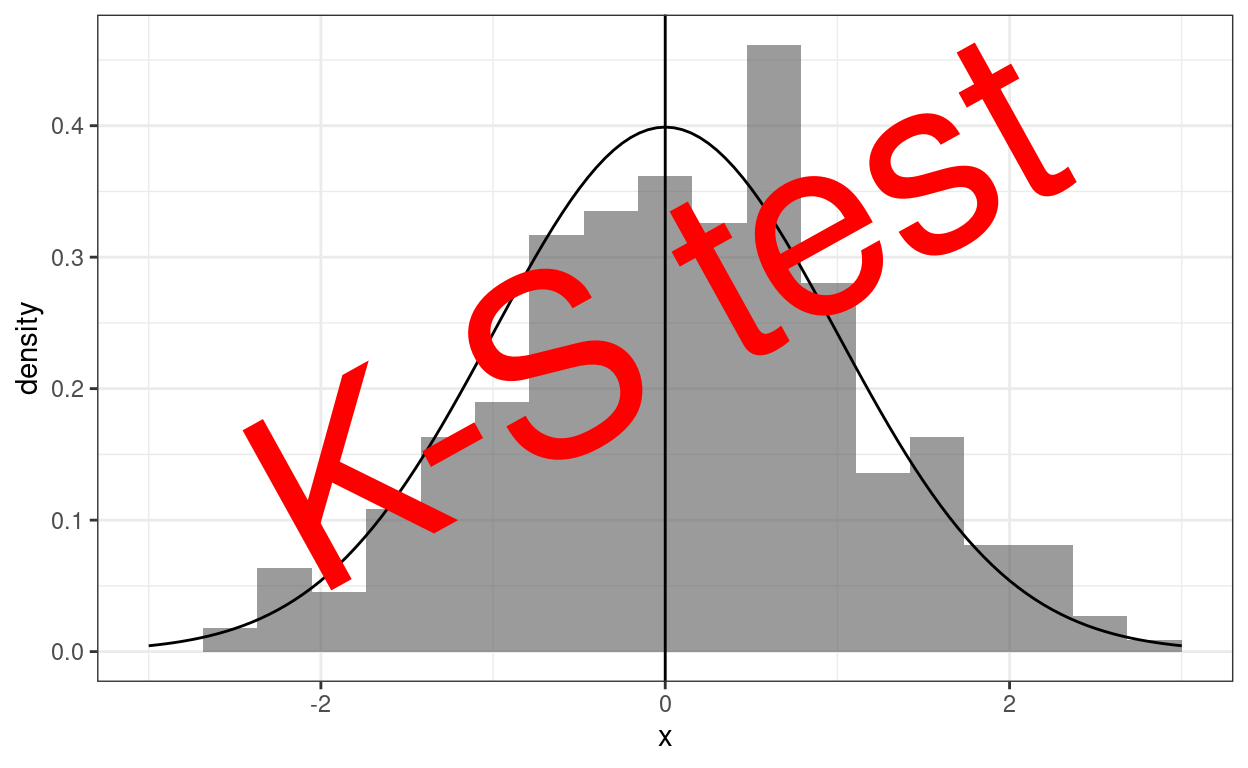
There are a number of situations in which we might want to test the fit of a distribution of values, say questionnaire scores and a distribution. That graph above shows a set of scores as a histogram and the standard Gaussian distribution shape superimposed on it. That’s a very crude eyeball test of fit to a distribution. Our eyeballs and brain aren’t very good at turning that into a more replicable way of assessing fit. Those methods are provided by tests of fit which ask: given a criterion of misfit, how unlikely is it, given the dataset size we have and the distribution it shows, that a misfit as large or larger than seen would have arisen by randomly sampling datasets of that size from the reference distribution.
Methodologically these situations fall into two groups:
- It may matter whether the distribution is a fit to a theoretical distribution, almost always the Gaussian distribution. These situations are called “one sample” testing as misfit of the one dataset to the theoretical distribution is tested.
- Sometimes we want to know if one empirical distribution is similar to another: is the distribution of scores on a questionnaire at assessment similar in our clinic to that reported from another clinic. These are “two sample” testing and perhaps underused in our field. The test here is whether the two samples differ too much on the misfit criterion to have plausibly been found by random sampling from the same population.
Why might we be wanting to do this? Taking them in reverse order, comparing the distributions between two samples goes beyond testing that the means for the two datasets might have come from populations with the same mean and helps us see if the distribution is different. Two clinics might have the same mean score but one have both more high scoring referrals and more low scoring referrals than the other. This could easily happen if referrers have different ideas about need and it could create very different pressures on the two clinics. However I don’t recall ever having seen this done in the therapy/MH literature (nor have I done it yet)!
What is much more common is that we see tests of fit to a distribution used to justify, or to reject, doing a subsequent, substantive analysis: testing for fit to Gaussian distribution before doing any of a long list of analyses: t-tests, ANOVAs, linear regression, multilevel analyses, factor analyses. This is quite a fraught area relating to “parametric statistics”. For many analyses the need for this pre-testing or prior exploration has reduced a bit with the increasing use of bootstrap analyses
Sadly, I think that far too often such “fit testing” becomes a sort of virtue signalling: “look we know what’s allowed and what isn’t” and is of rather little real help in ensuring that findings that are presented have their real robustness explored.
More positively, as long as its logic is understood, these are probably the most justifiable applications of Null hypothesis significance testing and the (NHST) paradigm for typical therapy/MH data.
Details #
For more on tests of fit it’s paradoxically best to go first to my Rblog post on the Kolmogorov-Smirnov test. That has graphics and examples that explain the K-S test. The K-S test is rather a nice test in its design and theory and was for many years the goto test of fit to a Gaussian distribution. However, it turns out to be a very poor test for that purpose. (It’s perhaps more interesting and useful for comparing two sets of assessment questionnaire scores.) That leads nicely into the next of my Rblog posts which is specifically on a set of better tests of fit.
Try also #
Kolmogorov-Smirnov test
Anderson-Darling test
Cramer von Mises test
Shapiro-Wilk test
Shapiro-Francia test
Null hypothesis testing
Distribution shape
Null hypothesis significance testing (NHST) paradigm
Sampling and sample frame
Population
Chapters #
The ideas of parametric and non-parametric tests, and hence of distributions and distribution testing crop up in Chapter 5 of the book.
Online resources #
See links in details above.
Dates #
First created 17.xi.23, updated links 20.xi.23.

